看完本篇文章,你可以解决下面四道”组合总和“的题目:
这四道题都属于Medium难度的题目,但是基本都可以用同一套思想和方法解决。
1.组合总和 & 组合总和 II
1.1 题目描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例:
输入:candidates = [2,7,6,3], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
「leetcode-39. 组合总和」 和 「leetcode-40. 组合总和 II」 想要解决的问题是类似的,只有两点细微的差别:
- 在第39题中,candidates数组中给定的元素是不重复的;而第40题中candidates数组中的元素可能是重复的;
- 在第39题中,candidates 中的数字可以无限制重复被选取;而第40题中candidates 中的每个数字在每个组合中只能使用一次。
1.2 题目分析
当我们遇到:“可行解是什么、可行解有多少个”这类问题时,最朴素的想法就是「枚举」,枚举出所有可能的结果,并在枚举的过程中不断删除不符合条件的解。
我们以问题39为例看看我们是怎么进行枚举的,以下图为例:
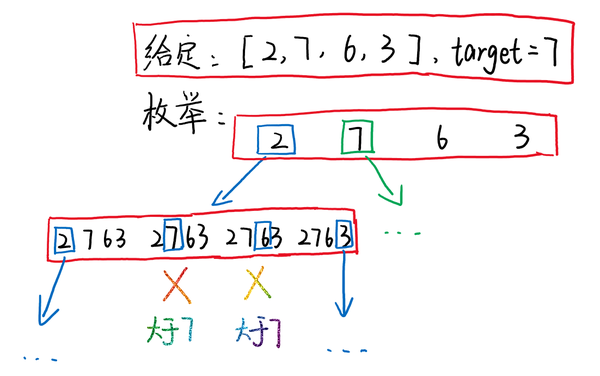
我们首先需要注意,题目中给了一个限定条件:所给的数都是正整数,这也就意味着数组中元素的加和是一个单调递增的值,所以当我们探索到[2,7]时,其和已经大于target(2+7>7),所以我们也没有必要继续往下探索,直接剪枝就可以。
所以枚举的本质就是「探索所有的可能性,留下满足条件解,删去不满足条件的解」。
当然我们发现,在上面枚举的过程中,我们可以对过程进一步优化。以上图为例,当我们枚举完 [2,7] 和 [2,6],并已经知道这两种方案不满足我们的要求时,我们依旧需要遍历7、6后面的元素,因为后面的元素可能比7,6小从而满足条件。
为了进一步优化我们的算法,我们可以将candidates数组先进行排序,然后再进行枚举的过程,如下图所示:
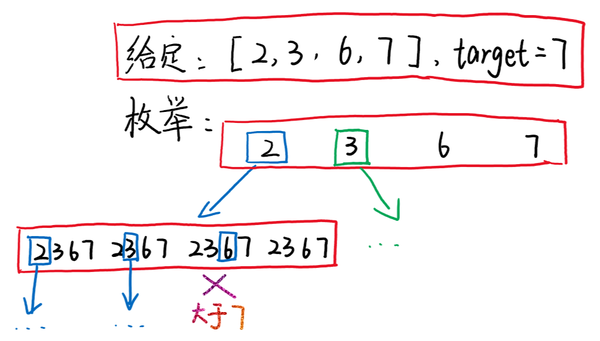
我们发现,当我们枚举到 [2, 6],并发现不满足条件时,6后面的元素我们已经不需要枚举了,因为其加和肯定比前面的大。这样的排序预处理可以降低我们算法的复杂度。
1.3 代码实现
枚举用编程的实现方式就是「回溯法」。
回溯有一个通用的模板,基本上可以套用到所有回溯的问题上,如下所示:
res = []
def backtrack(路径, 选择列表):
if 满足结束条件:
res.append(路径)
return
if 满足剪枝条件:
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
我们根据上述给定的回溯算法模板给出39题和40题的代码。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
if not candidates: #先解决空输入的情况
return []
candidates.sort() #排序
res=[]
def backtrack(i,temp_sum,temp_list):
"""
i:遍历到candidates数组中第几个元素
temp_sum:目前遍历数组的和
temp_list:目前遍历的数组
"""
if temp_sum==target:
res.append(temp_list)
return
if temp_sum>target:
return
for j in range(i,len(candidates)):
backtrack(j,temp_sum+candidates[j],temp_list+[candidates[j]])
backtrack(0,0,[])
return res
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
if not candidates:
return []
candidates.sort()
res=[]
def backtrack(i,temp_sum,temp_list):
if temp_sum==target:
res.append(temp_list)
return
if temp_sum>target or i==len(candidates):
return
for j in range(i,len(candidates)):
if j>i and candidates[j]==candidates[j-1]:#和39题不一样的地方,主要是为了防止出现重复的解
continue
backtrack(j+1,temp_sum+candidates[j], temp_list+[candidates[j]])
backtrack(0,0,[])
return res
我们发现第39题和第40题的解法基本一致。其实不只是上述的两个问题,基本上用枚举法可以解决的问题都可以尝试一下回溯法,就算不能AC,也能跑对部分样例。我们试着用给定的回溯法模板解决剩下的两个组合总和的问题。
2 组合总和 III & 组合总和 IV
2.1 组合总和 III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
「代码实现」
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
candidates = list(range(1,10))
res = []
def backtrack(i, temp_sum, temp_list):
if temp_sum==n and len(temp_list)==k:
res.append(temp_list)
return
if len(temp_list)==k:
return
for j in range(i, len(candidates)):
backtrack(j+1, temp_sum+candidates[j], temp_list+[candidates[j]])
backtrack(0,0,[])
return res
我们发现在这一题中,我们不需要对之前的回溯代码怎么修改,也是可以直接AC的。当然,我们可以进一步对代码做剪枝的优化,如下所示。
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
candidates = list(range(1,10))
res = []
def backtrack(i, temp_sum, temp_list):
if temp_sum==n and len(temp_list)==k:
res.append(temp_list)
return
if len(temp_list)==k:
return
for j in range(i, len(candidates)):
if len(temp_list)==k-1:
if temp_sum+candidates[j]>n or temp_sum+candidates[-1]<n: # 稍微优化了一下
break
backtrack(j+1, temp_sum+candidates[j], temp_list+[candidates[j]])
backtrack(0,0,[])
return res
2.2 组合总和 IV
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3]
target = 4
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
「代码实现」
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
if not nums:
return 0
res=[]
def backtrack(i,temp_sum,temp_list):
if temp_sum==target:
res.append(temp_list)
return
if temp_sum>target:
return
for j in range(len(nums)):
backtrack(j,temp_sum+nums[j],temp_list+[nums[j]])
backtrack(0,0,[])
return len(res)
我们发现,复用之前回溯的同一套代码,程序也是可以跑通。但因为回溯在很多时候就是一种比较懒惰的搜索方法,所以在这一题中,上述回溯的算法会显示超时,只能跑通部分样例。
在一般情况下,当我们使用回溯法显示算法超时的时候,我们可以往动态规划的角度思考,看动态规划是否可以解决这个问题,我给出这一题动态规划AC的代码。由于动态规划不是今天的重点,等后面做到动态规划相关题目的时候再给出总结。
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
"""
dp[i]:和为i的组合有多少个
"""
if not nums:
return 0
dp = [0] * (target+1)
dp[0] = 1
for i in range(1,target+1):
for num in nums:
if i >= num:
dp[i] += dp[i-num]
return dp[target]
课后题
以上就是这篇文章的全部内容,如果对你有帮助的话,欢迎点赞。你也可以继续挑战下面这些题目,都可以使用回溯法直接AC!相信做完下面几道题后,妈妈就再也不用怕你碰到回溯法啦!