这篇文章转载自我在知乎的文章
摘要
-
贝叶斯定理
-
朴素贝叶斯分类
-
半朴素贝叶斯分类
-
EM算法
-
代码实现与注释
贝叶斯定理
首先给出贝叶斯定理的公式:
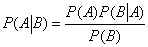
我个人觉得,贝叶斯公式其实就是条件概率的推广,每次想到贝叶斯公式,我就会在脑中冒出下面一幅图:
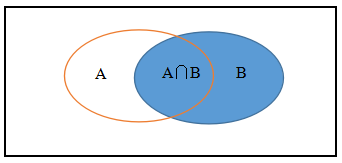
我们假设P(A)=1/3, P(B)=1/3, P(A∩B)=1/6.
条件概率\(P(A \mid B)\)就是在B发生的情况下,A发生的概率,即:
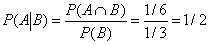
也就是说,在B发生时,A有1/2的可能性会发生,我们看上面的图,的确A∩B发生的可能性占到了B全部可能性的一半。
将上面的公式与贝叶斯公式进行对比,我们发现:
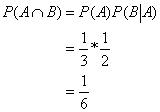
而条件概率和贝叶斯公式其实就是上述公式的转换。
朴素贝叶斯分类
那我们怎么来利用贝叶斯定理来进行分类呢?
我们首先假设有N种可能的分类类别,分别为{c1,c2,c3…cN},这时候对于样本x,我们利用贝叶斯定理:
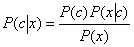
我们需要找到最大的$P(c\mid x)$作为样本x的最终分类,即:
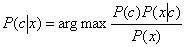
其中P(c)表示训练样本空间中各类样本所占的比例;$P(x\mid c)$表示类别为c的条件下,样本x的类条件概率;P(x)是用来归一化的“证据因子”,对于给定样本x,证据因子P(x)与类标记无关。
因此,估计$P(x\mid x)$的问题就转化为如何基于训练数据D来估计P(c)和$P(x\mid x)$。
P(c)很容易就可以得到,令Dc表示训练集D中第c类样本组成的集合,若有充足的独立同分布样本,则我们可以很容易估计出P(c)
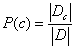
不难发现,基于贝叶斯公式,主要是$P(x\mid x)$比较难以求解,我们一般估计类条件概率主要使用极大似然估计法,但因为这里是所有属性上的联合概率,难以运用最大似然估计法直接估计得到。为了避开这个障碍,朴素贝叶斯分类器运用了“属性条件独立性假设”:对已知类别,假设所有属性相互独立。
基于上述假设,贝叶斯分类公式可以重写为:
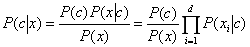
其中d为属性的数目,xi为样本x在第i个属性上的取值。
由于对所有的类别来讲,P(x)都相同,所以基于上式的贝叶斯判定准则为:
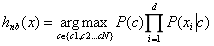
对于离散属性而言,令Dc,xi表示在第i个属性上取值为xi的样本组成的集合,则类条件概率可以估计为:
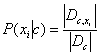
给大家举个例子:
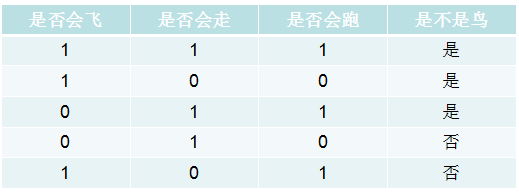
上面是训练样本,对于给定x样本={1,1,0},请问它是不是鸟?
首先我们估计先验概率P(c),有:
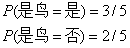
这时候我们为每个属性计算条件概率$P(x_i \mid c)$

于是,有

由于0.177>0.05,因此朴素贝叶斯分类将其判定为“是鸟”。
平滑处理
我们注意到,上面的计算过程存在一个弊端,那就是,如果某个属性值在训练集中没有与某个类同时出现过,则连乘时计算出的概率值为零。
为了让大家理解,还是用上面的例子,我把表格稍微改一下,如下:
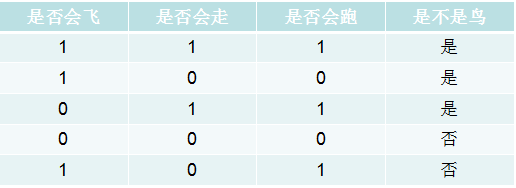
只对第四组数据做了一点改变,这时候我们计算测试例,有:

因此,无论该样本的其他属性是什么,“不是鸟”的概率都为零,分类结果都将是“是鸟=是”,这显然不合理。
为了避免上述弊端的出现,我们在计算概率值时要进行平滑处理,常用“拉普拉斯修正”:
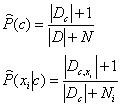
其中,N表示训练集D中可能出现的类别数,Ni表示第i个属性可能的取值数。拉普拉斯修正避免了因训练集样本不充分而导致的概率值为零的问题。
半朴素贝叶斯分类
我们在朴素贝叶斯分类中采用了“属性条件独立性假设”,但是在现实中,这个假设往往很难成立。
所以,半朴素贝叶斯分类的基本思想是适当考虑一部分属性间的依赖关系。
“独依赖估计”是半朴素贝叶斯分类中常用的一种策略。所谓的“独依赖”就是假设每个属性在类别之外最多依赖与其中一个属性,即
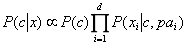
其中,pai是属性xi所依赖的属性,称为xi的父属性。
怎么来确定属性间的关系呢?一般有三种方法,分别是:SPODE、TAN、AODE.
我们这里主要讲一下TAN方法,另外两种方法想要了解的同学可以参照周志华老师《机器学习》P155.
TAN方法中最重要的一个判断标准就是两个属性间的条件互信息:
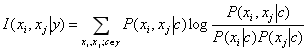
条件互信息刻画了属性xi和xj在已知类别下的相关性。我们需要找的,就是相关性大的属性。
EM算法
我们在现实中常常会遇到“不完整”的训练样本,在这种存在“未观测”变量的情形下,我们如何对模型参数进行估计?即如何用极大似然估计法计算模型参数。本算法与贝叶斯分类算法关系不大,这里我们仅对EM算法作简单介绍,想要详细了解的同学可以自行查阅资料。
我们定义未观测变量的学名是“隐变量”。令X表示已观测变量集,Z表示隐变量集,theta表示模型参数。
EM算法(参数最大化算法)是常用的估计参数隐变量的利器
其主要思想只有两步:
\1. 第一步是期望(E)步,利用当前估计的参数值来计算对数似然的期望值
\2. 第二步是最大化(M)步,寻找能使E步产生的似然期望最大化的参数值。然后,新得到的参数值重新被用于E步。
重复上述两步,直到收敛到局部最优解。就可以得到模型的参数。
上面就是贝叶斯分类的全部原理部分。
代码实现与注释
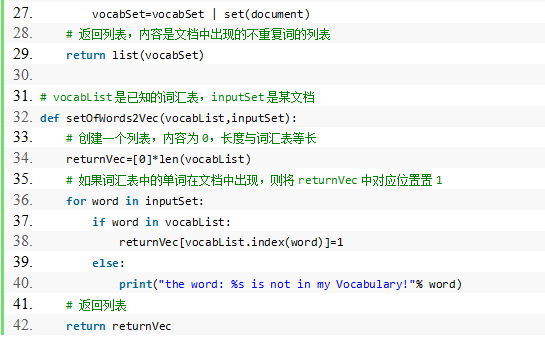
1.词表到向量的转换函数
程序清单:

\2. 朴素贝叶斯分类器训练函数
程序清单:


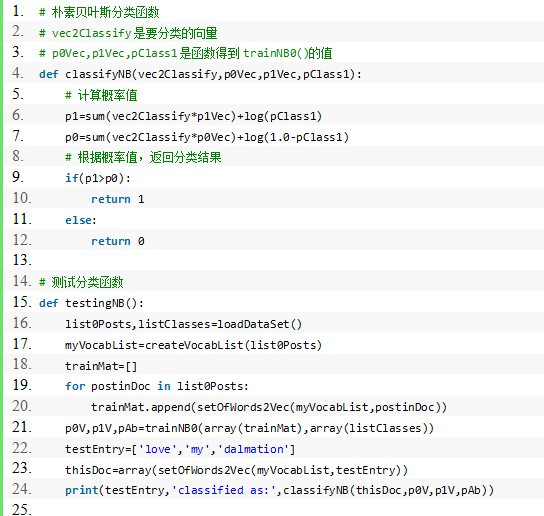
\3. 朴素贝叶斯分类函数
程序清单:
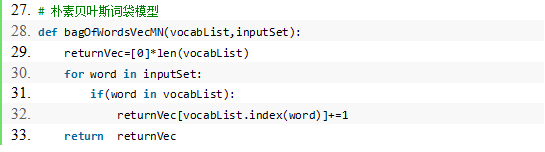
\4. 文本解析及垃圾邮件测试函数:
程序清单:


至此,我们完成了贝叶斯分类器原理和主要代码的学习。
下一节我们将进行Logistic回归的学习。
声明
最后,所有资料均本人自学整理所得,如有错误,欢迎指正,有什么建议也欢迎交流,让我们共同进步!转载请注明作者与出处。
以上原理部分主要来自于《机器学习》—周志华,《统计学习方法》—李航,《机器学习实战》—Peter Harrington。代码部分主要来自于《机器学习实战》,代码用Python3实现,这是机器学习主流语言,本人也会尽力对代码做出较为详尽的注释。