这篇文章转载自我在知乎的文章
摘要
1.k-均值聚类
2.二分k-均值聚类
3.代码实现与注释
k-均值聚类
首先说一下什么叫无监督学习。我们之前所讲的分类问题也好,回归问题也好,其样本的真实标记都是已经告诉我们的。但是无监督学习其训练样本并没有标记信息。
k-均值分类是无监督学习的一种,它想把给定数据划分为k类,这里的k是我们给定的参数。
k均值分类的工作流程是这样的:首先随机确定k个初始值作为质心,之后计算每个样本点到k个质心的距离,将样本分配给距离其最近的质心。这一步完成后,将k个类的质心更新为该类所有点的平均值。重复上述步骤,直到更新后聚类的结果不变。
其伪代码如下:

一般情况下,距离的度量我们可以用欧式距离:
二分k-均值聚类
k-均值聚类有时会收敛于局部最小值,如下图所示:
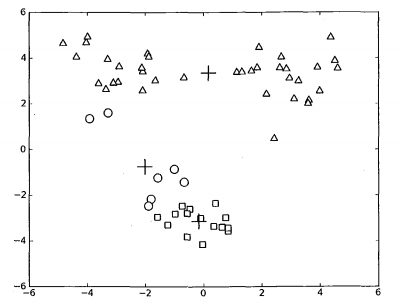
“+”代表分类中心,我们可以看到其分类的效果并不好,说明k-均值分类并没有让其收敛到全局最小值。
为了解决这个问题,发明了二分k-均值分类算法。
该算法首先将所有样本点作为一个簇,然后将该簇一分为二。之后选择其中一个簇继续划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低样本到质心的距离之和。划分完之后,这时已经将样本划分为了3簇,之后再选择一个簇继续划分。不断重复上述过程,直到簇数目的数量到达k个。
以上就是k-均值算法的全部原理部分,这个算法不难,希望能给大家帮助。下面是代码实现。
代码实现与注释
1.k-均值聚类函数
程序清单:
from numpy import *
# K均值聚类支持函数
# 数据加载
def loadDataSet(fileName):
dataMat=[]
fr=open(fileName)
for line in fr.readlines():
curLine=line.strip().split('\t')
fltLine=list(map(float,curLine))
dataMat.append(fltLine)
return dataMat
# 计算两个向量的距离
def distEclud(vecA,vecB):
return sqrt(sum(power(vecA-vecB,2)))
# 创建初始随机质点
def randCent(dataSet,k):
n=shape(dataSet)[1]
centroids=mat(zeros((k,n)))
for j in range(n):
minJ=min(dataSet[:,j])
rangeJ=float(max(dataSet[:,j]-minJ))
# 注意random.rand(k,1)返回的是k*1,数值在(0,1)之间的随机数
centroids[:,j]=minJ+rangeJ*random.rand(k,1)
return centroids
# k均值聚类算法
def kMeans(dataSet,k,distMeans=distEclud,createCent=randCent):
m=shape(dataSet)[0]
# 第一列存储簇索引值,第二列存储误差
clusterAssment=mat(zeros((m,2)))
# 初始化质心位置
cenrtroids=createCent(dataSet,k)
# 标志位
clusterChanged=True
while(clusterChanged):
clusterChanged=False
# 对每一个样本
for i in range(m):
# 初始化最小距离为无穷大,索引值为-1
minDist=inf;minIndex=-1
# 对每一个分类中心
for j in range(k):
# 计算距离
distJI=distMeans(cenrtroids[j,:],dataSet[i,:])
# 找到距离样本最近的分类中心
if(distJI<minDist):
minDist=distJI;minIndex=j
if(clusterAssment[i,0]!=minIndex):
clusterChanged=True
# 更新样本索引值和距离
clusterAssment[i,:]=minIndex,minDist**2
print(cenrtroids)
# 更新质心位置
for cent in range(k):
ptsInclust=dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
cenrtroids[cent,:]=mean(ptsInclust,axis=0)
return cenrtroids,clusterAssment
2.二分k-均值聚类
程序清单:
# 二分K均值聚类算法
def biKmeans(dataSet,k,disMeas=distEclud):
m=shape(dataSet)[0]
# 存储每个样本点的簇分配结果和平方误差
clusterAssment=mat(zeros((m,2)))
# 初始化质心
centroid0=mean(dataSet,axis=0).tolist()[0]
# centList列表中保留质心的位置
centList=[centroid0]
# 计算样本中所有点到质心的误差值
for j in range(m):
clusterAssment[j,1]=disMeas(centroid0,dataSet[j,:])**2
while(len(centList)<k):
lowestSSE=inf
# 遍历所有的簇
for i in range(len(centList)):
# 将簇类为i的点放到ptsIncurrCluster中
ptsIncurrCluster=dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
# 返回2分类的结果
centroidMat,splitClustAss=kMeans(ptsIncurrCluster,2,disMeas)
# 返回分类后的误差和
sseSplit=sum(splitClustAss[:,1])
# 得到剩余没划分的误差之和
sseNotSplit=sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
print("sseSplit,and :",sseSplit,sseNotSplit)
# 如果以i类二分之后的误差之后小于最小误差
if((sseSplit+sseNotSplit)<lowestSSE):
# 最好的划分簇为i
bestCentToSplit=i
# 新的质心
bestNewCents=centroidMat
bestClustAss=splitClustAss.copy()
# 更新簇的分配结果
bestClustAss[nonzero(bestClustAss[:,0].A==1)[0],0]=len(centList)
bestClustAss[nonzero(bestClustAss[:,0].A==0)[0],0]=bestCentToSplit
print("the bestCentTosplit is:",bestCentToSplit)
print("the len of bestClustAss is:",len(bestClustAss))
# 更新质心
centList[bestCentToSplit]=bestNewCents[0,:]
centList.append(bestNewCents[1,:])
clusterAssment[nonzero(clusterAssment[:,0].A==bestCentToSplit)[0],:]=bestClustAss
return mat(centList),clusterAssment
以上就是k-均值算法的全部内容,下一节我们一起学习概率图模型。
声明
最后,所有资料均本人自学整理所得,如有错误,欢迎指正,有什么建议也欢迎交流,让我们共同进步!转载请注明作者与出处
以上原理部分主要来自于《机器学习》—周志华,《统计学习方法》—李航,《机器学习实战》—Peter Harrington。代码部分主要来自于《机器学习实战》,我对代码进行了版本的改进,文中代码用Python3实现,这是机器学习主流语言,本人也会尽力对代码做出较为详尽的注释。