这篇文章转载自我在知乎的文章
摘要
-
线性支持向量机
-
非线性支持向量机和核函数
-
SMO算法
-
支持向量回归
-
代码实现与注释
上一节我们一起了解了支持向量机的基本概念、拉格朗日乘子法和对偶问题。这一节我们一起深入到支持向量机的具体问题及其解法。
线性支持向量机
1. 线性可分支持向量机
线性可分支持向量机是SVM中最简单最基本的形式,如下图(图片来自网络,侵删):
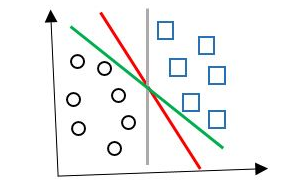
即通过一个超平面就可以完全将两个类别分开。
这种线性可分支持向量机的基本型:

首先我们利用拉格朗日乘子法引入拉格朗日函数:
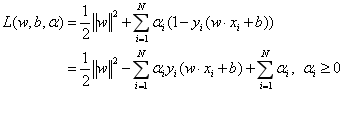
上一节讲过,原始问题的对偶问题就是极大极小问题:
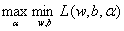
我们先求极小,再求极大:
(1)求min L(w,b,α)

将(1)式带入拉格朗日函数,并考虑(2)式的约束,得到:
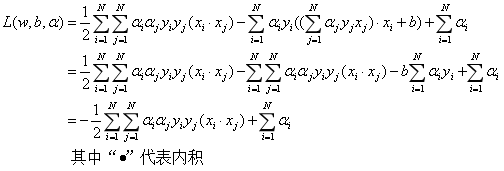
即:
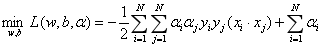
(2) 求L(w,b,α)对α的极大,即得:
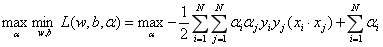
即可得到下列优化问题:
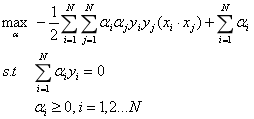
将目标函数由求最大值转换为求最小值,得到:
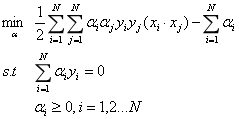
原始问题就转化为了上述对α的优化问题。
这时,我们假设求得了α的最优解:
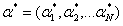
根据KKT条件,得:
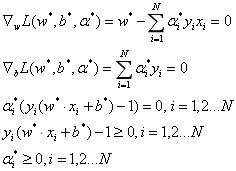
所以得:
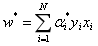
其中,至少有一个αj>0,(因为若所有的α都等于零,则w*等于零,则超平面不存在,矛盾),对此,对j有:
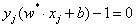
带入w*,得:
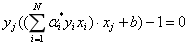
两边同乘yj,并考虑到(yj)2=1,得:
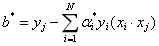
所以,我们可以由下式求得原始最优问题的解w和b:
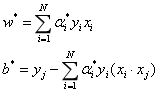
那分离超平面就可以写成:
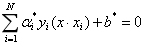
这就是说,分离超平面只依赖于输入x和训练样本的内积。
我们进一步可以发现,w和b只依赖于α>0的样本点,而其他样本点对w和b没有影响。我们又通过KKT约束条件:
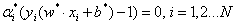
可知,对于α>0的样本i,其必定满足:
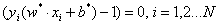
也就是说,样本点i位于间隔边界上,我们称它们为支持向量。这就得到了,分离超平面只与支持向量有关。
通过上述讨论,我们知道了线性可分数据的求解方式,那对于线性不可分数据我们应该怎么求解呢?
2.线性不可分支持向量机
其实在实际情况中,数据并不都是线性可分的,如下图(图片来自网络,侵删):
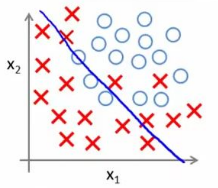
对于这样的数据集,我们刚刚的不等式约束不能对所有的样本点都成立。这时候,我们需要引入软间隔最大化的概念,将SVM推广到线性不可分数据问题。
线性不可分意味着有某些样本点(xi,yi)不能满足函数间隔大于等于1的约束条件,为了解决这个问题,我们为每个样本点引入一个松弛变量ξi>=0,使得函数间隔加上松弛变量大于等于1,得:
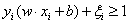
同时对每一个松弛变量支付一个代价,得到新的目标函数:
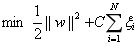
这里C>0,称为惩罚系数,C值大时表示对于错误分类的惩罚增大。
这时,线性不可分的问题就变成了如下优化问题:
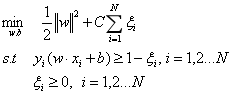
上述优化问题的拉格朗日函数为:
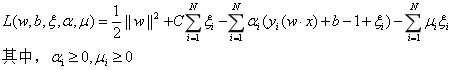
和线性可分支持向量机一样,对偶问题是极大极小问题。首先求L对w,b,ξ的极小,得:
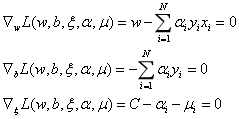
得到:
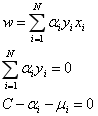
带入,得极小问题为:
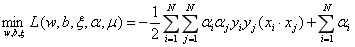
再对其求极大,得到对偶问题:
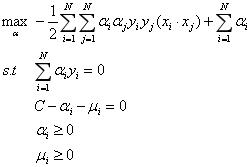
消去μ,得:
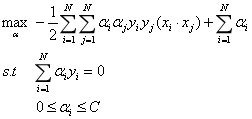
上式就是线性不可分问题的对偶问题。
同线性可分问题的求解方式,我们得到原始问题的解:
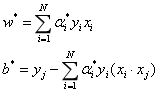
这时候可以得到分离超平面:
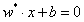
以上就是求解线性分类问题的线性支持向量机的方法。
非线性支持向量机和核函数
在之前的讨论中,我们用的数据都是线性可分的,即存在一个划分超平面可以将训练样本正确分类。但是有时候,并不存在这样的超平面能正确划分两类样本,如下图左图所示(图片来自于网络,侵删):
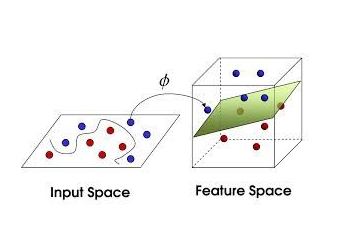
对于这样的问题,我们可以将输入空间映射到一个更高维的特征空间,使得样本在特征空间内线性可分。如上图的变换过程。
同时,我们可以证明,如果输入空间是有限维的,即属性有限,那么一定存在一个高维空间使得属性可分。

同样,类似上面的线性可分数据集,我们得到如下优化问题:

但由于特征空间的维数可能会很高,所以计算内积会比较困难。为了解决这个问题,我们定义了这样一个函数:
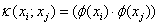
即xi和xj在特征空间的内积等于它们在输入空间中通过函数k(;)计算的结果。函数k(;)就称为核函数。有了这个函数,我们就不用去计算在高维空间的内积。
那么优化函数就可以重写为:
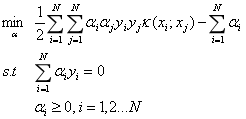
通过之前的讨论,在不知道特征映射的形式时,我们也就不知道什么样的核函数是合适的。于是,核函数的选取也就至关重要,如果核函数选取不佳,那么分类器的分类效果也就不会很好。这时,经验就比较重要。给大家一些常用的核函数有:线性核、高斯核、多项式核、拉普拉斯核、Sigmoid核等。
以上就是非线性支持向量机和核函数的基本概念。
SMO算法
大家发现,我们前面在解优化问题中的w和b时,总是先假设了参数α已经求得。那参数α怎么求呢?这就用到了SMO算法。
《机器学习实战》这本书中用代码实现了SMO算法,但是对于算法原理没有过多解释,所以读者可能会对代码中的公式很疑惑,在这里我给大家推一遍SMO算法,大家敲代码时可以对照着这部分的公式推导看。
序列最小最优化算法(SMO算法)是快速求解支持向量机的一种方法。它的实现手段是重复下面两步直到收敛:
\1. 选取一对需要更新的变量αi和αj;
\2. 固定αi和αj之外的参数,求解获得更新后的αi和αj。
我们要解如下优化问题:
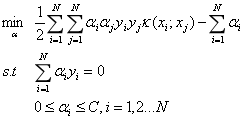
我们首先选取两个变量,不失一般性,选取变量α1和α2,其他变量αi固定,于是上述优化问题的子问题可以写成:
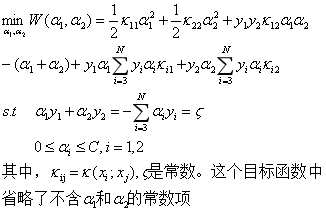
我们首先分析一下约束条件,因为有两个变量,约束可以用二维平面中的图形表示,如下:
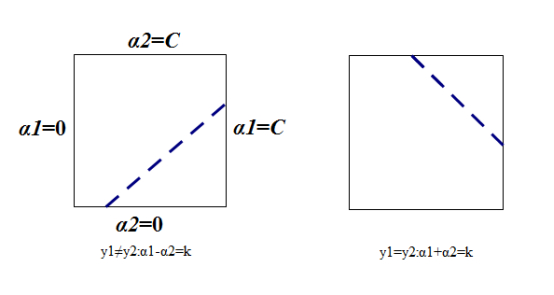
不等式约束使得两个变量在[0,C]*[0,C]内。因此要求目标函数在一条平行于对角线的线段上取最优值。这就使得两个变量的最优化问题实质上变成了单变量的最优化问题。不妨考虑为α2的最优化问题。
假设变量的初始解为α1old和α2old,最优解为α1new,α2new,所以:
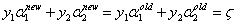
由于α2new需要满足不等式约束,所以其取值范围需要满足:
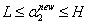
其中,L和H是上图对角端点的界,由上图可知:
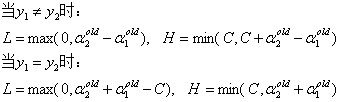
首先先考虑沿着约束方向未经剪辑即未考虑L和H约束时α2的最优解α2{new,unc};然后再求剪辑后α2的最优解α2{new}.
令:
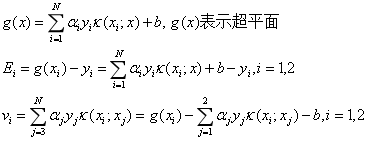
这时候目标函数可以写为:
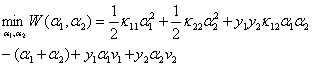
将α1带入上式,得到只有变量α2的目标函数:
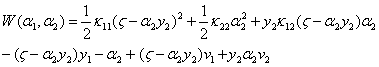
对α2求导得:
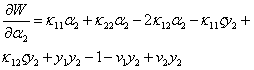
令其为零,得到:
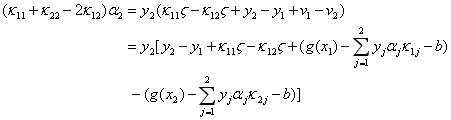
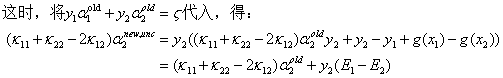
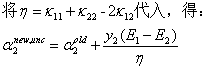
因为α2要满足约束条件L<=α2<=H,得到α2{new}如下表达式:
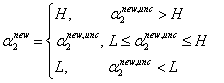
之后再得到α1{new}:
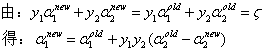
这时候就得到了两个参数的最优化解α1{new}和α2{new}。
变量选择
1. 第一个变量的选择
对于软间隔支持向量机,其KKT条件为:
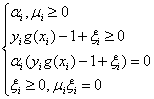

我们需要寻找的第一个变量就是违反KKT条件最严重的样本点。我们先遍历所有满足条件0<αi<C的样本点,即在间隔边界上的支持向量点,看他们是否满足KKT条件。如果这些样本点都满足,那么遍历整个数据集,找出不满足KKT条件的点。
2.第二个变量的选择
当我们已经选好第一个变量α1,这时第二个变量选择的标准就是希望能使α2有足够大的变化。
由之前得到:
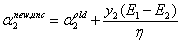
α2依赖于\(\|E_1-E_2\|\),所以一种简单的做法就是选择能使\(\|E_1-E_2\|\)最大的α2。
在特殊情况时,若上述方法选择的α2不能使目标函数有足够的下降,那么采用如下启发式的规则继续选择α2。首先遍历在间隔边界上的支持向量点,直到找到一个α2能使目标函数有足够的下降。若找不到合适的α2,那么遍历整个数据集;若仍找不到合适的α2,则放弃第一个α1,重新寻找一个α1.
3.计算b和差值Ei
当我们完成了两个变量的优化后,需要对b的值进行更新。

当我们更新完两个变量后,Ei的值同样需要更新:

重复上述步骤,直到α收敛,得到最优的α取值。
以上就是SMO算法的主要部分。
支持向量回归(SVR)
支持向量机不仅仅可以用于分类,其同样可以用于回归问题。
其和传统回归问题不同的地方在于,传统的回归模型是基于模型输出f(x)和真实输出y之间的差来计算损失,当且仅当f(x)和y完全相同时,损失才为零。
支持向量回归假设我们能容忍f(x)和y之间有ε的偏差,当且仅当f(x)和y之间的差值的绝对值大于ε时,才计算损失。
这一部分由于不是今天的重点,只是想提醒大家,支持向量机同样可以用于回归问题。想要详细了解的读者可以参阅周志华老师《机器学习》P133.
以上就是支持向量机全部的原理部分。
代码实现与注释
这部分代码内容涉及公式较多,建议配合SMO算法推导的公式一起看会很容易理解。
1.SMO算法中辅助函数
程序清单
from numpy import *
# 读取数据
def loadDataSet(filename):
dataMat=[];labelMat=[]
fr=open(filename)
for line in fr.readlines():
lineArr=line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
# 选择参数i之外的一个参数并返回
def selectJrand(i,m):
j=i
while(j==i):
j=int(random.uniform(0,m))
return j
# 调整aj的值
def clipAlpha(aj,H,L):
if(aj>H):
aj=H
if(L>aj):
aj=L
return aj
2.简化版SMO算法
程序清单:
# 简化版SMO算法
def smoSimple(dataMatIn,classLabels,C,toler,maxIter):
# 得到矩阵,将labelMat矩阵转置
dataMatrix=mat(dataMatIn);labelMat=mat(classLabels).transpose()
# 得到dataMatrix的大小
b=0;m,n=shape(dataMatrix)
# 初始化m*1的零矩阵
alphas=mat(zeros((m,1)))
iter=0
while(iter<maxIter):
# 初始化
alphaPairsChanged=0
# 对整个集合遍历
for i in range(m):
# 为第i个样本的预测类别。这一行代码看不懂的给大家一个链接,讲的很清楚
# http://www.bubuko.com/infodetail-694615.html
fxi=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:]))+b
# 计算预测出来的和真实的误差
Ei=fxi-float(labelMat[i])
# 如果误差比较大且alpha在0到C之间
if(((labelMat[i]*Ei<-toler)and(alphas[i]<C))or((labelMat[i]*Ei>toler)
and(alphas[i]>0))):
# 随机选取一个j
j=selectJrand(i,m)
# 同理,计算误差
fxj=float(multiply(alphas,labelMat).T*
(dataMatrix*dataMatrix[j,:]))+b
Ej = fxj - float(labelMat[j])
alphaIold=alphas[i].copy()
alphaJold=alphas[j].copy()
# 保证alpha在0到C之间
if(labelMat[i]!=labelMat[j]):
L=max(0,alphas[i]-alphas[j])
H=min(C,C+alphas[j]-alphas[i])
else:
L=max(0,alphas[j]+alphas[i]-C)
H=min(C,alphas[j]+alphas[i])
if(L==H):
print("L==H");continue
# 计算eta,下面这些公式看不懂没关系,会在正文部分给大家推导,大家对照着看
eta=(2.0*dataMatrix[i,:]*dataMatrix[j,:].T-dataMatrix[i,:]*
dataMatrix[i,:].T-dataMatrix[j,:]*dataMatrix[j,:].T)
if(eta>=0):
print("eta>=0")
continue
alphas[j]-=labelMat[j]*(Ei-Ej)/eta
alphas[j]=clipAlpha(alphas[j],H,L)
if(abs(alphas[i]-alphaJold)<0.00001):
print('j is not moving enough')
continue
alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j])
b1=(b-Ei-labelMat[i]*(alphas[i]-alphaIold)*
dataMatrix[i,:]*dataMatrix[i,:].T-
labelMat[j]*(alphas[j]-alphaJold)*
dataMatrix[i,:]*dataMatrix[j,:].T)
b2=(b-Ej-labelMat[i]*(alphas[i]-alphaIold)*
dataMatrix[i,:]*dataMatrix[j,:].T-
labelMat[j]*(alphas[j]-alphaJold)*
dataMatrix[j,:]*dataMatrix[j,:].T)
if((0<alphas[i])and(C>alphas[i])):
b=b1
elif((0<alphas[j])and(C>alphas[j])):
b=b2
else:b=(b1+b2)/2.0
alphaPairsChanged+=1
print("iter: %d i %d,pairs changed %d"%(iter,i,alphaPairsChanged))
if(alphaPairsChanged==0):iter+=1
else:iter=0
print('itertion number: %d'% iter)
return b,alphas
3.完整版SMO支持函数
程序清单:
# 完整版SMO支持函数
class optStruct:
def __init__(self,dataMatIn,classLabels,C,toler,Ktup):
self.X=dataMatIn
self.labelMat=classLabels
self.C=C
self.m=shape(dataMatIn)[0]
self.alphas=mat(zeros((self.m,1)))
self.b=0
# eCache中第一列为标志位,第二列是误差E值
self.eCache=mat(zeros((self.m,2)))
self.tol=toler
self.K=mat(zeros(self.m,self.m))
for i in range(self.m):
self.K[:,i]=kernelTrans(self.X,self.X[i,:],kup)
def calcEk(oS,k):
# 计算预测值
fXk=float(multiply(oS.alphas,oS.labelMat).T*
(oS.X*oS.X[k,:].T))+oS.b
# 计算误差
Ek=fXk-float(oS.labelMat[k])
return Ek
# 选择第二个alpha
def selectJ(i,oS,Ei):
maxK=-1;maxDeltaE=0;Ej=0
# 将输入值在eCache中设置为有效
oS.eCache[i]=[1,Ei]
# 返回非零E值的位置
validEcacheList=nonzero(oS.eCache[:,0].A)[0]
if((len(validEcacheList))>1):
# 选择误差E最大的
for k in validEcacheList:
if k==i:continue
Ek=calcEk(oS,k)
deltaE=abs(Ei-Ek)
if(deltaE>maxDeltaE):
maxK=k
maxDeltaE=deltaE
Ej=Ek
return maxK,Ej
# 如果是第一次循环,就随机挑选一个j
else:
j=selectJrand(i,oS.m)
Ej=calcEk(oS,j)
return j,Ej
# 更新eCache中的误差值
def updateEk(oS,k):
Ek=calcEk(oS,k)
oS.eCache[k]=[1,Ek]
4.完整的SMO优化例程
程序清单:
# 完整的SMO的优化例程
# 其和上面简化版的基本一致,公式部分看不懂看正文
def innerL(i,oS):
Ei=calcEk(oS,i)
if((oS.labelMat[i]*Ei<-oS.tol)and(oS.alphas[i]<oS.C)or
(oS.labelMat[i] * Ei>oS.tol) and (oS.alphas[i] >0)):
j,Ej=selectJ(i,oS,Ei)
alphaIold=oS.alphas[i].copy()
alphaJold=oS.alphas[j].copy()
if(oS.labelMat[i]!=oS.labelMat[j]):
L=max(0,oS.alphas[j]-oS.alphas[i])
H=min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i]-oS.C)
H = min(oS.C,oS.alphas[j] + oS.alphas[i])
if(L==H):print('L==H');return 0
eta=(2.0*oS.X[i,:]*oS.X[j,:].T-oS.X[i,:]*oS.X[i,:].T-
oS.X[j,:]*oS.X[j,:].T)
if(eta>=0):print("eta>=0");return 0
oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta
oS.alphas[j]=clipAlpha(oS.alphas[j],H,L)
updateEk(oS,j)
if((abs(oS.alphas[j]-alphaJold)<0.00001)):
print('j not moving enough')
return 0
oS.alphas[i]+=oS.labelMat[j]*oS.labelMat[i]*(alphaJold-oS.alphas[j])
updateEk(oS,i)
b1=(oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*
oS.X[i,:]*oS.X[i,:].T-oS.labelMat[j]*
(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS[j,:].T)
b2 = (oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) *
oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] *
(oS.alphas[j] - alphaJold) * oS.X[j, :] * oS[j, :].T)
if((0<oS.alphas[i])and(oS.C>oS.alphas[i])):
oS.b=b1
elif((0<oS.alphas[j])and(oS.C>oS.alphas[j])):oS.b=b2
else:oS.b=(b1+b2)/2.0
return 1
else:
return 0
# 完整版SMO的外循环代码
def smoP(dataMatIn,classLabels,C,toler,maxIter,kTup=('lin',0)):
oS.optStruct(mat(dataMatin),mat(classLabels).transpose(),C,toler)
iter=0
entireSet=True;alphaPairsChanged=0
while((iter<maxIter)and((alphaPairsChanged>0)or(entireSet))):
alphaPairsChanged=0
if(entireSet):
for i in range(oS.m):
alphaPairsChanged+=innerL(i,oS)
print('fullSet iter : %d i:%d,pairs changed %d'%
(iter,i,alphaPairsChanged))
iter+=1
else:
nonBoundIs=nonzero((oS.alphas.A>0)*(oS.alphas.A<C))[0]
for i in nonBoundIs:
alphaPairsChanged+=innerL(i,oS)
print("non-bound,iter:%d i:%d,pairs changed %d"%
(iter,i,alphaPairsChanged))
iter+=1
if(entireSet):
entireSet=False
elif(alphaPairsChanged==0):
entireSet=True
print('iteration number: %d'%iter)
return oS.b,oS.alphas
def calWs(alphas,dataArr,classLabels):
X=mat(dataArr);labelMat=mat(classLabels).transpose()
m.n=shape(X)
w=zeros((n,1))
for i in range(m):
w+=multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
以上就是支持向量机(SVM)全部的内容。这个算法推导部分公式较多,但其实自己推导一遍并不是很难,同时也会加深自己对于算法的理解。推导过程中一些注意要点我也都写了出来,希望能给大家提供一点帮助。下一节一起梳理AdaBoost元算法。
声明
最后,所有资料均本人自学整理所得,如有错误,欢迎指正,有什么建议也欢迎交流,让我们共同进步!转载请注明作者与出处。
以上原理部分主要来自于《机器学习》—周志华,《统计学习方法》—李航,《机器学习实战》—Peter Harrington。代码部分主要来自于《机器学习实战》,代码用Python3实现,这是机器学习主流语言,本人也会尽力对代码做出较为详尽的注释。